(本小题满分16分)在四棱锥 中,
中, 平面
平面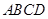 ,
, 是正三角形,
是正三角形,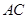 与
与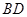 的交点
的交点 恰好是
恰好是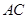 中点,又
中点,又 ,
,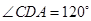 ,点
,点 在线段
在线段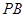 上,且
上,且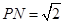 .
.
(1)求证: ;
;
(2)求证: ∥平面
∥平面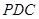 ;
;
(3)求二面角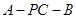 的余弦值.
的余弦值.
已知函数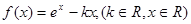
(Ⅰ)若 试确定函数
试确定函数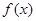 的单调区间;
的单调区间;
(Ⅱ)若 ,且对于任意
,且对于任意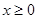 ,
,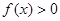 恒成立,求实数
恒成立,求实数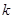 的取值范围;
的取值范围;
(Ⅲ)令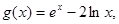 若至少存在一个实数
若至少存在一个实数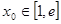 ,使
,使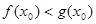 成立,求实数
成立,求实数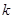 的取值范围.
的取值范围.
定义在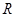 上的函数
上的函数
 ,当
,当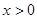 时,
时,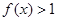 ,且对任意的
,且对任意的 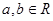 ,有
,有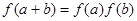 ,
,
(Ⅰ)求证: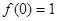 ;
;
(Ⅱ)求证:对任意的 ,恒有
,恒有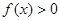 ;
;
(Ⅲ)证明: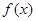 是
是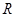 上的增函数.
上的增函数.
已知函数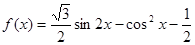 ,
,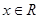 .
.
(Ⅰ)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足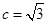 ,
, 且
且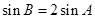 ,求
,求 、
、 的值.
的值.
将一颗骰子先后抛掷2次,观察向上的点数,求:
(Ⅰ)两数之和为5的概率;
(Ⅱ)两数中至少有一个为奇数的概率.
如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱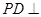 底面ABCD,
底面ABCD,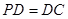 ,E是PC的中点.
,E是PC的中点.
(Ⅰ)证明  平面EDB;
平面EDB;
(Ⅱ)求EB与底面ABCD所成的角的正切值.