(本小题满分12分)己知A、B、C是椭圆C: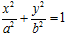 (a>b>0)上的三点,其中点A的坐标为
(a>b>0)上的三点,其中点A的坐标为 ,BC 过椭圆的中心,且
,BC 过椭圆的中心,且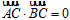 ,
,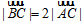 .
.
(1)求椭圆C的方程;
(2)过点(0,t)的直线l(斜率存在时)与椭圆C交于P,Q两点,设D为椭圆C与y轴负半轴的交点,且 ,求实数t的取值范围.
,求实数t的取值范围.
(本小题满分12分)在锐角△ABC中,角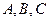 的对边分别为
的对边分别为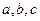 ,且满足
,且满足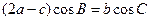 . (Ⅰ)求角B的大小; (Ⅱ)设
. (Ⅰ)求角B的大小; (Ⅱ)设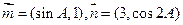 ,试求
,试求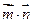 的取值范围.
的取值范围.
.(本小题满分12分)设命题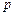 :关于
:关于 的不等式
的不等式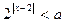 的解集为
的解集为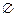 ;命题
;命题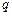 :函数
:函数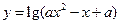 的值域是
的值域是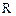 .如果命题
.如果命题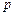 和
和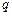 有且仅有一个正确,求实数
有且仅有一个正确,求实数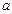 的取值范围.
的取值范围.
(本小题满分14分)
设函数 ,
,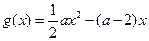 ,
,
(1)对于任意实数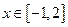 ,
,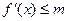 恒成立,求
恒成立,求 的最小值;
的最小值;
(2)若方程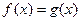 在区间
在区间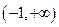 有三个不同的实根,求
有三个不同的实根,求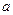 的取值范围.
的取值范围.
(本小题满分14分)
等差数列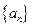 前
前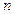 项和为
项和为 ,已知对任意的
,已知对任意的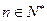 ,点
,点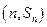 在二次函数
在二次函数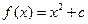 图象上。
图象上。
(1)求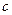 ,
,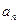 ;
;
(2)若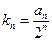 ,求数列
,求数列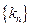 前
前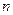 项和
项和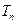 .
.
(本小题满分14分)
已知椭圆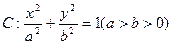 的离心率为
的离心率为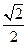 ,且曲线过点
,且曲线过点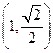
(1)求椭圆C的方程;(2)已知直线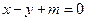 与椭圆C交于不同的两点A,B,且线段AB的中点不在圆
与椭圆C交于不同的两点A,B,且线段AB的中点不在圆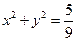 内,求
内,求 的取值范围.
的取值范围.