学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )

| A.1000 | B.900 | C.100 | D.90 |
设命题P:关于x的不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同;命题Q: 。则命题Q()
。则命题Q()
| A.是命题P的充分必要条件 |
| B.是命题P的充分条件但不是必要条件 |
| C.是命题P的必要条件但不是充分条件 |
| D.既不是命题P的充分条件也不是命题P的必要条件 |
使关于 的不等式
的不等式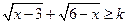 有解的实数
有解的实数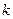 的最大值是()
的最大值是()
A.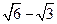 |
B.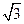 |
C. |
D. |
顶点为P的圆锥的轴截面是等腰直角三角形,A是底面圆周上的点,B是底面圆内的点,O为底面圆的圆心,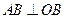 ,垂足为B,
,垂足为B,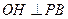 ,垂足为H,且PA=4,C为PA的中点,则当三棱锥O-HPC的体积最大时,OB的长是()
,垂足为H,且PA=4,C为PA的中点,则当三棱锥O-HPC的体积最大时,OB的长是()
A.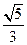 |
B. |
C.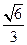 |
D.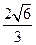 |
已知如图的曲线是以原点为圆心,1为半径的圆的一部分,则这一曲线的方程是( )
A.(x+ )(y+ )(y+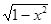 )=0 )=0 |
B.(x- )(y- )(y-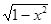 )=0 )=0 |
C.(x+ )(y- )(y-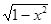 )=0 )=0 |
D.(x- )(y+ )(y+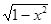 )=0 )=0 |
直线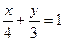 椭圆
椭圆 相交于A,B两点,该椭圆上点P,使得⊿PAB面积等于3,这样的点P共有
相交于A,B两点,该椭圆上点P,使得⊿PAB面积等于3,这样的点P共有
| A.1个 | B.2个 | C.3个 | D.4个 |