已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线为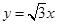 ,右焦点
,右焦点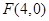 ,左右顶点分别为
,左右顶点分别为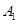 ,
, ,
,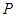 为双曲线上一点(不同于
为双曲线上一点(不同于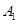 ,
, ),直线
),直线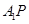 ,
,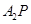 分别与直线
分别与直线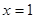 交于
交于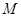 ,
, 两点;
两点;
(1)求双曲线的方程;
(2)求证: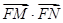 为定值,并求此定值.
为定值,并求此定值.
已知函数 .
.
(1)画出函数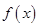 的图象,写出函数
的图象,写出函数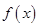 的单调区间;
的单调区间;
(2)解关于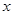 的不等式
的不等式
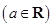 .
.
极坐标方程为 的直线与
的直线与 轴的交点为
轴的交点为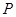 ,与椭圆
,与椭圆  (
(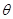 为参数)交于
为参数)交于 求
求 .
.
(本小题满分10分)
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.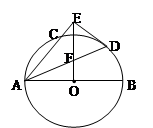
(1)求证:DE是⊙O的切线;
(2)若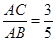 ,求
,求 的值.
的值.
(本小题满分12分)已知数列 各项均不为0,其前
各项均不为0,其前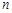 项和为
项和为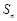 ,且对任意
,且对任意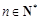 都有
都有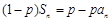 (
(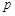 为大于1的常数),记
为大于1的常数),记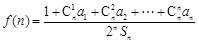 .
.
(1) 求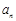 ;
;
(2) 试比较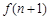 与
与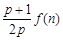 的大小(
的大小(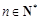 );
);
(3) 求证:
(本小题满分12分)己知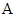 、
、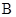 、
、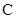 是椭圆
是椭圆 :
: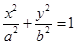 (
(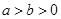 )上的三点,其中点
)上的三点,其中点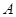 的坐标为
的坐标为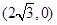 ,
,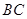 过椭圆的中心,且
过椭圆的中心,且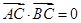 ,
,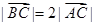 。
。
(Ⅰ)求椭圆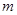 的方程;
的方程;
(Ⅱ)过点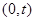 的直线
的直线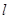 (斜率存在时)与椭圆
(斜率存在时)与椭圆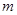 交于两点
交于两点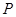 ,
,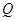 ,设
,设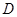 为椭圆
为椭圆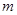 与
与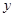 轴负半轴的交点,且
轴负半轴的交点,且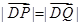 ,求实数
,求实数 的取值范围.
的取值范围.