某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化调整第一个月的销售价,预计销售定价每增加1元,销售量将减少10套。
(1)若设第二个月的销售定价每套增加x元,填写下表。
| 时间 |
第一个月 |
第二个月 |
| 每套销售定价(元) |
|
|
| 销售量(套) |
|
|
(2)若商店预计要在这两个月的代销中获利4160元,则第二个月销售定价每套多少元?
先化简,再求值: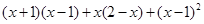 ,其中
,其中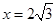 .
.
(本题12分)如图①所示,在正方形ABCD中,M是AB的中点,E是AB的延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.
(1)求证:MD=MN;
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”,其余条件不变,如图②所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.
(本题12分)某楼盘一楼是车库(暂不销售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
(1)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式;
(2)小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(3)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体的数据阐明你的看法.
(本题10分)某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表
| 类别 |
人数 |
占总人数比例 |
| 重视 |
a |
0.3 |
| 一般 |
57 |
0.38 |
| 不重视 |
b |
c |
| 说不清楚 |
9 |
0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?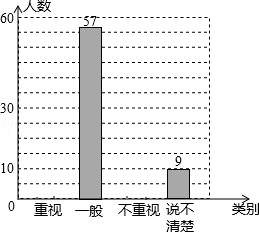
(本题11分)矩形纸片ABCD的长AD为4cm,宽AB为3cm,把矩形纸片拼叠,使相对两顶点A,C重合,然后展开,求折痕EF的长.