已知,如图:四边形ABCD中,∠C>90°,CD⊥AD于D,CB⊥AB于B,AB= ,tanA是关于x的方程
,tanA是关于x的方程 的一个实数根。
的一个实数根。
(1)求tanA;
(2)若CD=m,求BC的值。
有一枚均匀的正方体骰子,6个面上分别标有数字1~6,随意掷出这枚骰子,求下列事件发生的概率掷出的数字恰好是1的概率
掷出的数字恰好是奇数的概率
掷出的数字大于4的概率。
掷出的数字大于7的概率
掷出的数字不小于3的概率
如图,已知∠C=∠D,DB∥EC.AC与DF平行吗?试说明你的理由.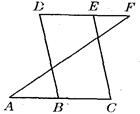
尺规作图(不写作法,但要保留作图痕迹)
如图7,点E为∠ABC边BC上一点,过点E作直线MN,使MN//AB.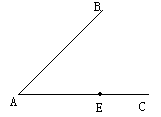
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下: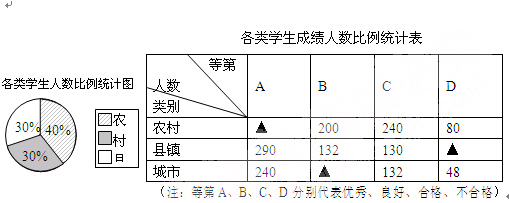
请将上面表格中缺少的三个数据补充完整
若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数
化简 (3a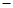 2)2
2)2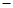 (3a
(3a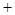 2)2
2)2