化简 (3a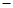 2)2
2)2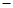 (3a
(3a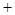 2)2
2)2
如图,已知L1⊥L2,⊙O与L1,L2都相切,⊙O的半径为1cm,矩形ABCD的边AD、AB分别与直线L1,L2重合,∠BCA=600,若⊙O与矩形ABCD沿L1同时向右移动,⊙O的移动速度为2cm/s,矩形ABCD的移动速度为3cm/s,设移动时间为t(s)
(1)如图①,连接OA、AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,求当对角线AC所在直线与圆O第二次相切 时t的值。
如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E,
(1)判断△FBC的形状,并说明理由;
(2)请探索线段AB、AC与AF之间满足条件的关系式并说明理由.
)已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E。
(1)求证:DE是⊙O的切线;
(2)作DG⊥AB交⊙O于G点,垂足为F点,若∠A=30°,AB=8,求DG的长。
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D(如图)
(1)求证:AC=BD
(2)若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长.