如图,平面上一点P从点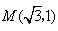 出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长
出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长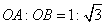 ;过点O且垂直于射线OM的直线
;过点O且垂直于射线OM的直线 与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
(1)在点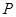 运动过程中,试判断AB与y轴的位置关系,并说明理由.
运动过程中,试判断AB与y轴的位置关系,并说明理由.
(2)设点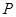 与直线L都运动了t秒,求此时的矩形OAPB与直线
与直线L都运动了t秒,求此时的矩形OAPB与直线 在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).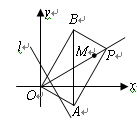
(1)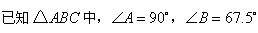 ,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)

王大伯要做一张如图1的梯子,梯子共有8级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度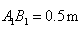 ,最下面一级踏板的长度
,最下面一级踏板的长度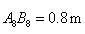 .木工师傅在制作这些踏板时,截取的木板要比踏板长,以保证在每级踏板的两个外端各做出一个长为4cm的榫头(如图2所示),以此来固定踏板.现市场上有长度为2.1m的木板可以用来制作梯子的踏板(木板的宽厚和厚度正好符合要制作梯子踏板的要求),请问:制作这些踏板,王大伯最少需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)
.木工师傅在制作这些踏板时,截取的木板要比踏板长,以保证在每级踏板的两个外端各做出一个长为4cm的榫头(如图2所示),以此来固定踏板.现市场上有长度为2.1m的木板可以用来制作梯子的踏板(木板的宽厚和厚度正好符合要制作梯子踏板的要求),请问:制作这些踏板,王大伯最少需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)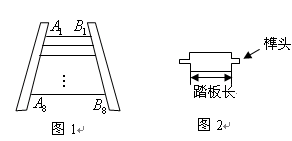
小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图像如图中的折线段OA-OB所示.
(1)试求折线段OA-OB所对应的函数关系式;
(2)请解释图中线段AB的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离 (千米)与小明出发后的时间
(千米)与小明出发后的时间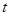 (分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为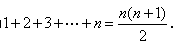
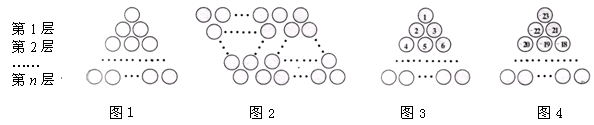
如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,
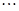 ,则最底层最左边这个圆圈中的数是;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,
,则最底层最左边这个圆圈中的数是;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,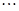 ,求图4中所有圆圈中各数的绝对值之和.
,求图4中所有圆圈中各数的绝对值之和.