如图所示,长为L、内壁光滑的直管与水平地面成300角固定放置。将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km的小物块相连,小物块悬挂于管口。现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变.(重力加速度为g)
(1)求小物块下落过程中的加速度大小;
(2)求小球从管口抛出时的速度大小;
(3)试证明小球平抛运动的水平位移总小于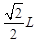
如图所示,在范围很大的水平向右的匀强电场中,一个电荷量为-q的油滴,从A点以速度v竖直向上射人电场.已知油滴质量为m,重力加速度为g,当油滴到达运动轨迹的最高点时,测得它的速度大小恰为v/2,问:
电场强度E为多大?
A点至最高点的电势差为多少?
如图所示,一束电子从静止开始经U′= 5000V的电场加速后,从水平放置的一对平行金属板正中水平射入偏转电场中,若金属极板长L = 0.05m,两极板间距d = 0.02m,试求: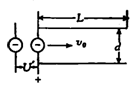
两板间至少要加U才能使电子恰不飞出电场?
在上述电压下电子到达极板时的动能。
用30cm的细线将质量为4×10-3㎏的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为1×104N/C的匀强电场时,小球偏转37°后处在静止状态。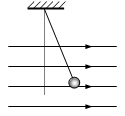
分析小球的带电性质
求小球的带电量
求细线的拉力
跳伞运动员做低空跳伞表演,他离开飞机后先做自由落体运动,当距离地面 125 m时打开降落伞,伞张开后运动员就以14.3 m/s2的加速度做匀减速运动,到达地面时速度为5 m/s,问:运动员离开飞机时距地面的高度为多少?
离开飞机后,经过多少时间才能到达地面?(g="10" m/s2)
一石子从楼顶由静止开始下落,不计空气阻力,现测得石子在最后1 s内下落的高度是25 m,求楼有多高?(g=10m/s2)