如图所示,无限宽广的匀强磁场分布在xoy平面内,x轴上下方磁场均垂直xoy 平面向里,x轴上方的磁场的磁感应强度为B,x轴下方的磁场的磁感应强度为4B/3。现有一质量为m,电量为-q带负电粒子以速度v0从坐标原点O沿y方向进入上方磁场。在粒子运动过程中,与x轴交于若干点。不计粒子的重力。求: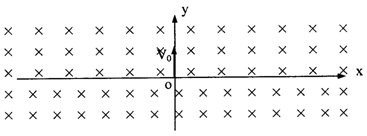
(1)粒子在x轴上方磁场做匀速圆周运动半径r1
(2)如把x上方运动的半周与x下方运动的半周称为一周期的话,则每经过一周期,在x轴上粒子右移的平均速度。
(3)在与x轴的所有交点中,粒子两次通过同一点的坐标位置。
水平放置的平行金属板AB间的距离d=0.1m,板长L=0.3m,在金属板的左端竖直放置一带有小孔的挡板,小孔恰好位于AB板的正中间,距金属板右端x=0.5m处竖直放置一足够大的荧光屏,现在AB板间加如图(b)所示的方波形电压,已知U0=1.0×102V,在挡板的左侧,有大量带正电的相同粒子以平行于金属板方向的速度持续射向挡板,粒子的质量m=1.0×10-7kg,电荷量q=1.0×10-2C,速度大小均为v0=1.0×104m/s,带电粒子的重力不计,则: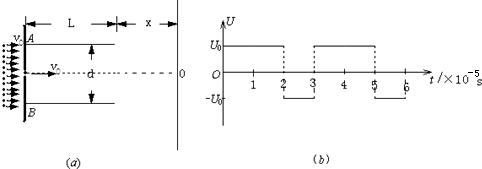
(1)求粒子在电场中的运动时间;
(2)求在t=0时刻进入的粒子打在荧光屏上的位置到O点的距离;
(3)请证明粒子离开电场时的速度均相同;
(4)若撤去挡板,求荧光屏上出现的光带长度。
如图所示,A为电解槽(电能转化为化学能的装置),M为电动机,N为电炉子,恒定电压U=12V,电解槽内阻rA=2Ω,当K1闭合,K2、K3断开时,电流表示数I1=6A;当K2闭合,K1、K3断开时,电流表示数I2=3A,且电动机输出功率为13.5W;当K3闭合,K1、K2断开时,电流表示数为I3=2A.不计电流表内阻,求:
(1)电炉子的电阻R及发热功率PR;
(2)电动机的内阻rM;
(3)在电解槽工作时,电能转化为化学能的功率P化。
从电子枪射出初速度不计的电子束,如图所示,经电压U1=180V的加速电场加速后,从正中间平行进入金属板Y和Y′,电子束穿过两板后最终垂直打在荧光屏上的O点.若现在用一输出电压为U2=160V的稳压电源与金属板YY′连接,在YY′间产生匀强电场,使得电子束发生偏转.若取电子质量为m=9×10﹣31kg,带电量e=1.60×10﹣19C,YY′两板间距d=9.0cm,板长l=9.0cm,板的末端到荧光屏的距离L=13.5cm.整个装置处于真空中,不考虑重力的影响,试回答以下问题:
(1)电子束射入金属板YY′时速度v0;
(2)加上电压U2后电子束打到荧光屏上的位置到O点的距离y′;
(3)如果两金属板YY′间的距离d可以随意调节(保证电子束仍从两板正中间射入),其他条件都不变,试求电子束打到荧光屏上的位置到O点距离的取值范围.
如图示电路中,电阻R1=R2=6Ω,R3=4Ω,R4=3Ω。电源内阻r=2Ω。不计电压表和电流表的影响。S断开时,电压表的示数为2.25V。求: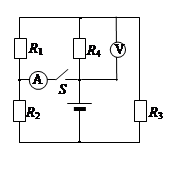
(1)电源电动势E;
(2)S合上后,电流表的示数。
如图所示,A为电解槽(电能转化为化学能的装置),N为电炉子,恒定电压U=12V,电解槽内阻rA=2Ω,当K1闭合,K2断开时,电流表示数I1=6A;当K2闭合,K1断开时,电流表示数为I2=2A.不计电流表内阻,求:
(1)电炉子的电阻R及发热功率PR;
(2)在电解槽工作时,电能转化为化学能的功率P化。