)阅读下面的材料,回答问题:
爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题。例如: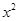 -6x+10=(
-6x+10=(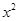 -6x+9-9)+10=
-6x+9-9)+10=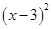 -9+10=
-9+10=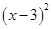 +1≥1;因此
+1≥1;因此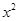 -6x+10有最小值是1;
-6x+10有最小值是1;
(1)尝试:-3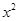 -6x+5=-3(
-6x+5=-3(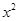 +2x+1-1)+5=-3
+2x+1-1)+5=-3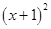 +8,因此-3
+8,因此-3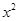 -6x+5有最大值是______
-6x+5有最大值是______
(2)应用:有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成一个的长方形花圃。能围成面积最大的花圃吗?如果能,请求出最大面积.
不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为 .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心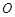 ,另一边所在直线与半圆相交于点
,另一边所在直线与半圆相交于点 ,量出半径
,量出半径 ,弦
,弦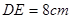 ,求这把直尺的宽度.
,求这把直尺的宽度.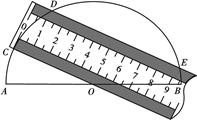
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,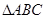 的顶点均在格点上,点
的顶点均在格点上,点 的坐标为
的坐标为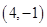
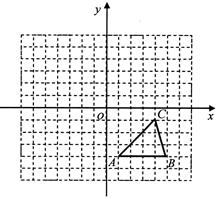
(1)在方格纸中作出与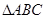 关于原点对称的
关于原点对称的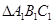 ;
;
(2)直接写出过A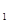 、B
、B 、O三点的抛物线的对称轴;
、O三点的抛物线的对称轴;
(1)解方程:
(2)已知二次函数y=x2+bx-3的图像经过点(-2,5),请求出这个函数的解析式,并直接写出当自变量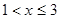 时函数值
时函数值 的取值范围.
的取值范围.
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0),
(1)请直接写出点A关于原点O对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,求出A′点的坐标。
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.