如图，在矩形OABC中，OA=3，OC=5，分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数
（
）的图象经过点D且与边BA交于点E，连接DE．
（1）连接OE，若△EOA的面积为2，则k= ；
（2）连接CA，DE与CA是否平行？请说明理由；
（3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．
已知：如图，在△ABC中，AB=AC，AD⊥BC垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E，DE交AC于点F.
（1）求证：四边形ADCE是矩形；
（2）猜想线段DF和AB有何数量关系，并说明理由；
（3）直接写出当△ABC满足什么条件时，四边形ADCE是正方形？
甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发去乙地．如图，线段OA表
示货车离甲地距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地距离y（km）
与时间x（h）之间的函数关系．请根据图象，解答下列问题：
（1）线段CD表示轿车在途中停留了 小时；
（2）求线段DE对应的函数解析式；
（3）求轿车从甲地出发后经过多长时间追上货车．
如图，学校为美化校园，将形状是直角三角形的一园地△ABC，分别以三边AB、CA、BC为直径向外作半圆，开辟为三个花坛甲、乙、丙，现分给八年一班同学种花。班长准备让人数相等的两个小组同学负责。为了公平分配任务，她安排一个小组负责花坛甲，另一个小组负责花坛乙和丙。你认为班长的安排合理吗？请说明理由．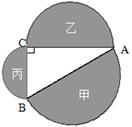
如图，在□ABCD中，AB=2 BC=4，点E、F分别是BC、AD的中点．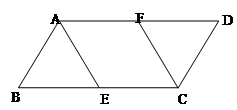
（1）求证：△ABE≌△CDF；
（2）当四边形AECF为菱形时，求出该菱形的面积．
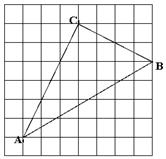
已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，△ABC
的顶点在格点上，称为格点三角形，试判断△ABC的形状．请说明理由．