(本小题满分14分)
已知 是椭圆
是椭圆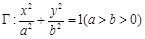 的左右焦点,椭圆
的左右焦点,椭圆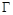 的离心率
的离心率 ,
, 是
是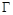 上异于左右顶点的任意一点,且
上异于左右顶点的任意一点,且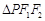 的面积的最大值为1.
的面积的最大值为1.
(Ⅰ)求椭圆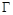 的方程;
的方程;
(Ⅱ)直线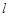 是椭圆在点P处的切线,过
是椭圆在点P处的切线,过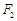 作
作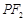 的垂线,交直线
的垂线,交直线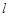 相交于Q,求证:点Q落在一条定直线
相交于Q,求证:点Q落在一条定直线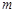 上,并求直线
上,并求直线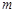 的方程.
的方程.
(文科)已知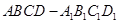 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高 .求:
.求:
⑵异面直线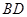 与
与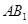 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);
⑵ 四面体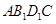 的体积.
的体积.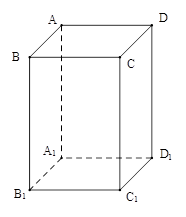
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为 ,容器的高为
,容器的高为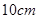 .制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到
.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到 )
)
本题共有3个小题,第1小题满分5分,第2小题满分6分,
第3小题满分7分.
对定义在区间 上的函数
上的函数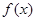 ,若存在闭区间
,若存在闭区间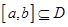 和常数
和常数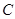 ,使得对任意的
,使得对任意的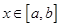 都有
都有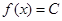 ,且对任意的
,且对任意的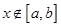 都有
都有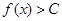 恒成立,则称函数
恒成立,则称函数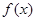 为区间
为区间 上的“U型”函数。
上的“U型”函数。
(1)求证:函数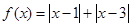 是
是 上的“U型”函数;
上的“U型”函数;
(2)设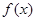 是(1)中的“U型”函数,若不等式
是(1)中的“U型”函数,若不等式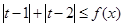 对一切的
对一切的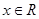 恒成立,
恒成立,
求实数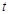 的取值范围;
的取值范围;
(3)若函数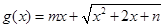 是区间
是区间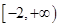 上的“U型”函数,求实数
上的“U型”函数,求实数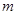 和
和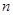 的值.
的值.
本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分.
设 把三阶行列式
把三阶行列式 中第一行第二列元素的余子式记为
中第一行第二列元素的余子式记为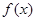 ,且关于
,且关于 的不等式
的不等式 的解集为
的解集为 。各项均为正数的数列
。各项均为正数的数列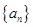 的前
的前 项和为
项和为 ,点列
,点列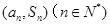 在函数
在函数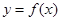 的图象上。
的图象上。
(1)求函数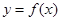 的解析式;
的解析式;
(2)若 ,求
,求 的值;
的值;
(3)令 ,求数列
,求数列 的前
的前 项中满足
项中满足 的所有项数之和.
的所有项数之和.
本题共有2个小题,第1小题满分8分,第2小题满分6分.
为保护环境,某单位采用新工艺,把二氧化碳转化为一种可利用的化工产品。已知该单位每月的处理量最多不超过300吨,月处理成本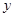 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系式可近似的表示为:
(吨)之间的函数关系式可近似的表示为: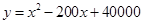 ,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)要保证该单位每月不亏损,则每月处理量应控制在什么范围?