如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2)。
(1)请在图中画出△ABC关于y轴的轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直写出D、E、F的坐标。
(2)求四边形ABED的面积。
为了解某校“振兴阅读工程”的开展情况,教育部门对该校初中生的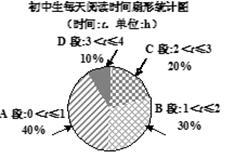

阅读情况进行了随机问卷调查,绘制了如下图表:
初中生喜爱的文学作品种类调查统计表
| 种类 |
小说 |
散文 |
传记 |
科普 |
军事 |
诗歌 |
其他 |
| 人数 |
72 |
8 |
21 |
19 |
15 |
2 |
13 |
根据上述图表提供的信息,解答下列问题:
(1)喜爱小说的人数占被调查人数的百分比是多少?初中生每天阅读时间的中位数在哪
个时间段内?
(2)将写读后感、笔记积累、画圈点读等三种方式称为有记忆阅读.请估计该校现有的
2000名初中生中,能进行有记忆阅读的人数约是多少?
根据我省“十二五”铁路规划,连云港至徐州客运专线项目建成后,连云港至徐州的最短客运时间将由现在的2小时18分缩短为36分钟,其速度每小时将提高260km.求提速后的火车速度.(精确到1km/h)
两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分△AOF与△DOC是否全等?为什么?
解不等式组: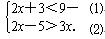
解方程: .
.