如图,小李在一次高尔夫球选拔赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30o,O、A两点相距8 米.
米.
(1)求直线OA的解析式;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小李这一杆能否把高尔夫球从O点直接打入球洞A点.
(本小题满分8分)小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片 放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知
放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知 =36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
(本题共两小题,每小题6分,满分12分)
(1)计算: .
.
(2)解不等式组,并把解集在数轴上表示出来.

(本小题满分12分)如图1,已知抛物线经过坐标原点 和
和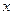 轴上另一点
轴上另一点 ,顶点
,顶点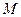 的坐标为
的坐标为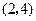 ;矩形
;矩形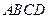 的顶点
的顶点 与点
与点 重合,
重合, 分别在
分别在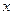 轴、
轴、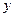 轴上,且
轴上,且 ,
, .
.
(1)求该抛物线所对应的函数关系式;
(2)将矩形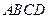 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿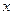 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点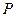 也以相同的速度从点
也以相同的速度从点 出发向
出发向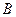 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为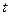 秒(
秒( ),直线
),直线 与该抛物线的交点为
与该抛物线的交点为 (如图2所示).
(如图2所示).
①当 时,判断点
时,判断点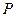 是否在直线
是否在直线 上,并说明理由;
上,并说明理由;
②设以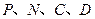 为顶点的多边形面积为
为顶点的多边形面积为 ,试问
,试问 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
(本小题满分12分)如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点 E.
(1) 求∠AEC的度数;
(2)求证:四边形OBEC是菱形.
(本小题满分10分)袋中装有除数字不同其它都相同的六个小球,球上分别标有数字1,2,3,4,5,6.
(1)从袋中摸出一个小球,求小球上数字小于3的概率;
(2)将标有1,2,3数字的小球取出放入另外一个袋中,分别从两袋中各摸出一个小球,求数字之和为偶数的概率.(要求用列表法或画树状图求解)