小明和小亮进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡底跑到坡顶再原路返回坡底.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小明在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).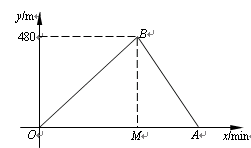
(1)求小明上、下坡的速度及A点的坐标;
(2)小亮上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
某校九(1)、九(2)两班的班长交流了为四川安雅地震灾区捐款的情况:
(Ⅰ)九(1)班班长说:“我们班捐款总数为1200元,我们班人数比你们班多8人.”
(Ⅱ)九(2)班班长说:“我们班捐款总数也为1200元,我们班人均捐款比你们班人均捐款多20%.”
请根据两个班长的对话,求这两个班级每班的人均捐款数.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.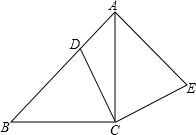
(1)求证:AB⊥AE;
(2)若BC2=AD•AB,求证:四边形ADCE为正方形.
为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.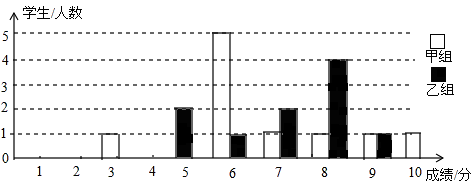
(1)补充完成下面的成绩统计分析表:
| 组别 |
平均分 |
中位数 |
方差 |
合格率 |
优秀率 |
| 甲组 |
6.7 |
3.41 |
90% |
20% |
|
| 乙组 |
7.5 |
1.69 |
80% |
10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转装盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得元购物券,最多可得元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.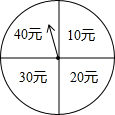
已知关于x、y的方程组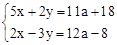 的解满足x>0,y>0,求实数a的取值范围.
的解满足x>0,y>0,求实数a的取值范围.