为鼓励大学毕业生自主创业，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：
．
（1）李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？
（2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？
如图，△ABC中，点D在BC的延长线上，过D作DE⊥AB于E，交AC于F。已知∠A=30°，∠FCD=80°，求∠D的度数。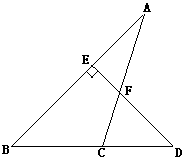
在图所示的平面直角坐标系中表示下面各点：。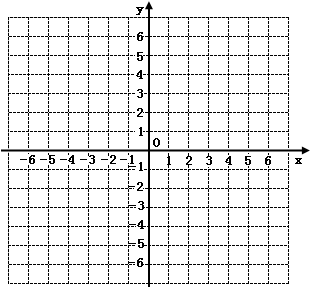
A（0，3），B（1，－3），C（3，－5），D（－3，－5），E（3，5），F（5，7）。
（1）A点到原点O的距离是__ __个单位长。
（2）将点C向左平移6个单位，它会与点重合。
（3）连接CE，则直线CE与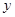
轴是什么位置关系？
（4）点F到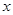
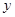、轴的距离分别是多少？
如图，A点在B处的北偏东40°方向，C点在B处的北偏东85°方向，A点在C处的北偏西45°方向，求∠BAC及∠BCA的度数？。
若∣m＋n－5∣＋（2m＋3n－5）2＝0，求（m＋n）2的值。
已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数。