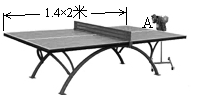
（本题12分）某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，假设每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球运行时，设乒乓球与端点A的水平距离为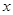
（米），与桌面的高度为
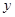（米），运行时间为
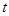（秒），经多次测试后，得到如下部分数据：2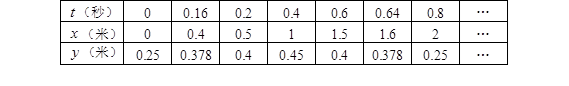
（1）当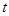为何值时，乒乓球达到最大高度？
（2）乒乓球落在桌面时，与端点A的水平距离是多少？
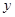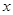（3）乒乓球落在桌面上弹起后，与满足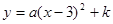
．
①用含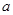
的代数式表示
；
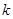②球网高度为0.14米，球桌长（1.4×2）米，若球弹起后，恰好有唯一的击球点，可以将球沿直线扣杀到点A，求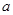的值．
．
，求作△ABC，使得BC = a，AC = b，
．（不写作法，保留作图痕迹）．
；
；
……
