配方法可以用来解一元二次方程，还可以用它来解决很多问题。例如：因为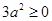
，所以
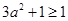，即：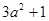
有最小值1，此时
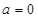；同样，因为
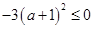，所以
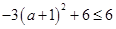，即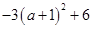
有最大值6，此时
。
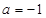①当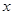
= 时，代数式
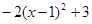有最 （填写大或小）值为 。②当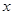= 时，代数式
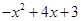有最 （填写大或小）值为 。
③矩形花园的一面靠墙，另外三面的栅栏所围成的总长度是16m，当花园与墙相邻的边长为多少时，花园的面积最大？最大面积是多少？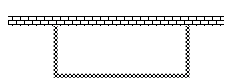
（本小题满分6分）在平面直角坐标系xOy中，直线y=kx+4（k≠0）与y轴交于点A.
（1）如图，直线y=－2x+1与直线y=kx+4（k≠0）交于点B，与y轴交于点C，点B的横坐标为-1.
①求点B的坐标及k的值；
②直线y=－2x+1、直线y=kx+4与y轴所围成的△ABC的面积等于；
（2）直线y=kx+4（k≠0）与x轴交于点E（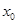
,0）,若-2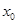＜＜-1，求k的取值范围.
（本小题满分6分）若等腰△ABC的一边长为a=2，另外两边长b、c恰好是关于x的一元二次方程
－（m+3）x+m+2=0的两个根，求△ABC的周长.
（本小题满分6分）在一只不透明的布袋中装有红球、黄球各若干个，这些球除颜色外都相同，充分摇匀.
（1）已知这只布袋中有3个红球，1个黄球.从袋中一次摸出2个球，计算“摸出的球恰是一红一黄”的概率（用“画树状图”或“列表”的方法写出计算过程）.
（2）若这只布袋中有3个红球，x个黄球.
请写出一个x的值，使得事件“从袋中一次摸出4个球，都是黄球”是不可能事件.
（本小题满分4分）如图AB是半圆的直径.图1中，点C在半圆外；图2中，点C在半圆内.请仅用无刻度的直尺按要求画图．
（1）在图1中，画出△ABC的三条高的交点；
（2）在图2中，画出△ABC中AB边上的高．
（本小题满分10分）
（1）解方程：
；
（2）解不等式：
≤
，并将它的解集在数轴上表示出来.