已知△ABC中,A,B,C所对的边分别为a,b,c,已知m=(sin C,sin Bcos A),n=(b,2c),且m·n=0.
(1)求A的大小;
(2)若a=2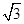 ,c=2,求△ABC的面积S的大小.
,c=2,求△ABC的面积S的大小.
已知函数 是增函数,
是增函数, 为减函数.
为减函数.
(1)求a的值;
(2)设函数 上的增函数,且对于
上的增函数,且对于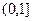 内的任意两个变量s、t,
内的任意两个变量s、t, 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(3)设 ,求证:
,求证: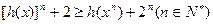
已知直线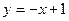 与椭圆
与椭圆 相交于A、B两点.
相交于A、B两点.
(1)若椭圆的离心率为 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)若向量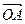 与向量
与向量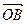 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率 时,求椭圆的长轴长的最大值
时,求椭圆的长轴长的最大值
已知函数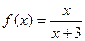 ,数列
,数列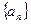 满足
满足 ,
,
(1)求数列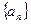 的通项公式
的通项公式 ;
;
(2)若数列 满足
满足 ,求
,求
在一次语文测试中,有一道把我国近期新书:《声涯》、《关于上班这件事》、《长尾理论》、《游园惊梦:昆曲艺术审美之旅》与它们的作者连线题,已知连对一个得3分,连错一个不得分,一位同学该题得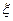 分.
分.
(1)求该同学得分不少于6分的概率;
(2)求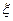 的分布列及数学期望.
的分布列及数学期望.
已知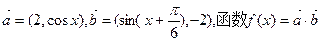 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)若 的值
的值