“直线
垂直于平面a内的无数条直线”是“⊥a”的（）
| A．充分条件 | B．必要条件 |
| C．充要条件 | D．既不充分也不必要条件 |
a和b是两条异面直线，下列结论正确的是( )
| A．过不在a、b上的任意一点，可作一个平面与a、b都平行 |
| B．过不在a、b上的任意一点，可作一条直线与a、b都相交 |
| C．过不在a、b上的任意一点，可作一条直线与a、b都平行 |
| D．过a可以并且只可以作一个平面与b平行 |
直线a∥平面?，平面?内有n条直线相交于一点，那么这n条直线中与直线a平行的( )
| A．至少有一条 | B．至多有一条 |
| C．有且只有一条 | D．不可能有 |
直线a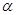∥面
，面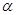内有n条互相平行的直线，那么这n条直线和直线a( )
| A．全平行 | B．全异面 |
| C．全平行或全异面 | D．不全平行也不全异面 |
m、n是平面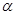
外的两条直线，在m∥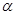的前提下，m∥n是n∥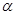的( )
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
在（0，+∞）内为增函数，且
也为增函数，则
的取值范围是（ ） 
