(本题满分6分,)小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下面各题:
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出4张卡片,用学过的运算方法,使结果为24.如何抽取?写出运算式子(一种即可)
答:(1)我抽取的2张卡片是____________ 、____________ 、
乘积的最大值为____________ .
(2)我抽取的4张卡片是___________ 、____________ 、___________ 、____________ ,
算24的式子为__________________________________________.
如图,在梯形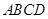 中
中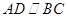 ,
,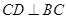 ,已知
,已知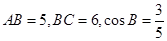 ,点
,点 为
为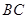 边上的动点,连接
边上的动点,连接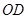 ,以
,以 为圆心,
为圆心, 为半径的⊙
为半径的⊙ 分别交射线
分别交射线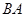 于点
于点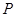 ,交射线
,交射线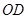 于点
于点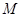 ,交射线
,交射线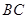 于
于 ,连接
,连接 .
.
(1)求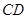 的长.
的长.
(2)当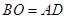 时,求
时,求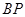 的长.
的长.
(3)在点 的运动过程中,
的运动过程中,
①当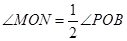 时,求⊙
时,求⊙ 的半径.
的半径.
②当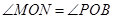 时,求⊙
时,求⊙ 的半径(直接写出答案).
的半径(直接写出答案).
某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量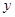 (万件)与销售单价
(万件)与销售单价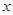 (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数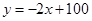 .(利润=售价-制造成本)
.(利润=售价-制造成本)
(1)写出每月的利润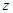 (万元)与销售单价
(万元)与销售单价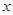 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
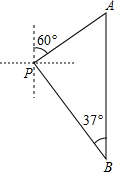
周末,小亮一家在瘦西湖游玩,妈妈在岸边 处观看小亮与爸爸在湖中划船(如图).小船从
处观看小亮与爸爸在湖中划船(如图).小船从 处出发,沿北偏东60°划行300米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到1米)?(参考数据:
处出发,沿北偏东60°划行300米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到1米)?(参考数据: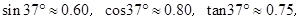
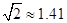 ,
,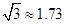 )
)
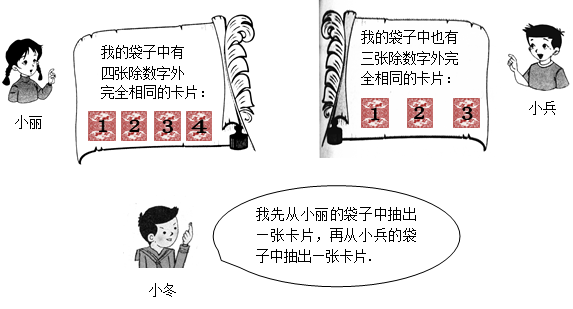
阅读对话,解答问题.
(1) 分别用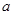 、
、 表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用
表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用
树状图法或列表法写出(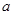 ,
, ) 的所有取值;
) 的所有取值;
(2) 求点(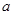 ,
, )在一次函数
)在一次函数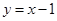 图像上的概率.
图像上的概率.