为提供节约用水,某市按如下规定每月收取水费,若一户居民每月用水不超过20立方米,则每立方米按3元收费;若超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费,若某户居民某月用水x立方米.
(1)试用含x的代数式表示这户居民该月应缴的水费(分两种情况).
(2)已知该市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家一季度应缴纳水费多少元?
(1)四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如下图1,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5,求中间小正方形的面积.
(2)现有一张长为6.5cm,宽为2cm的纸片,如图9,请你将它分割成6块,再拼合成一个正方形.(要求:先在图2中画出分割线,再画出拼成的正方形并标明相应数据)

如图,四边形ABCD是菱形,对角线AC=8 cm , BD=6 cm, DH⊥AB于H,求:DH的长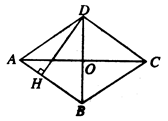
从旗杆的顶端系一条绳子,垂到地面还多2米,小敏拉起绳子下端绷紧,刚好接触地面,发现绳子下端距离旗杆底部8米,小敏马上计算出旗杆的高度,你知道她是如何解的吗?
已知,如图所示,正方形ABCD,E、M、F、N分别是AD、AB、BC、CD上的点,若EF⊥MN,求证:EF=MN.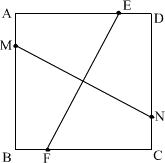
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)每件衬衫降价多少元时,商场平均每天赢利最多?