问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,根据SAS,易证△AFG≌△AFE,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】
如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( -1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
-1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: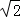 =1.41,
=1.41, =1.73)
=1.73)

一只蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记为“+”,向负半轴运动记为“—”,从开始到结束爬行的各段路程(单位:cm)依次为+7,—5,—10,—8,+9,—6,+12,+4。
(1)若A点在数轴上表示的数为—2,则蜗牛停在数轴上何处,请通过计算加以说明。
(2)若蜗牛的爬行速度为每秒 ,请问蜗牛一共爬行了多少秒?
,请问蜗牛一共爬行了多少秒?
若 、
、 互为相反数,
互为相反数, 、
、 互为倒数,
互为倒数, 的绝对值等于2,计算
的绝对值等于2,计算 的值。
的值。
(1)化简
(2)先化简,再求值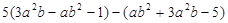 ,其中
,其中 ,
,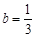
如图,直线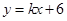 与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).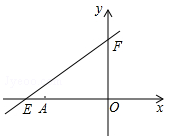
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点, 当点P运动过程中,试写出三角形OPA的面积s与x的函数关系式,并写出自变量x的取值范围;
当点P运动过程中,试写出三角形OPA的面积s与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为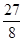 ,并说明理由.
,并说明理由.
甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,先填好下表,再写出总运费y关于x的函数关系式;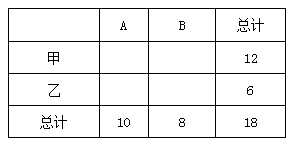
(2)若要求总运费不超过900元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?