一只蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记为“+”,向负半轴运动记为“—”,从开始到结束爬行的各段路程(单位:cm)依次为+7,—5,—10,—8,+9,—6,+12,+4。
(1)若A点在数轴上表示的数为—2,则蜗牛停在数轴上何处,请通过计算加以说明。
(2)若蜗牛的爬行速度为每秒 ,请问蜗牛一共爬行了多少秒?
,请问蜗牛一共爬行了多少秒?
已知a,b互为相反数,c,d互为倒数,x是64的立方根,求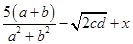 的值.
的值.
完成证明:(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b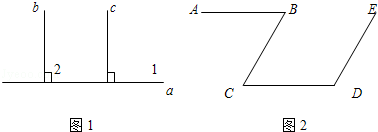
证明:∵a⊥c
∴∠1=________
∵b∥c
∴∠1=∠2( )
∴∠2=∠1=90°
∴a⊥b ;
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE
证明:∵AB∥CD (已知)
∴∠B=________( )
∵∠B+∠D="180°" (已知)
∴∠C+∠D="180°" ( )
∴CB∥DE( )
如图,已知AB∥CE,∠A=∠E,证明:∠CGD=∠FHB.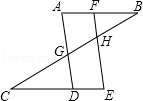
计算下列各题
(1) (2)
(2)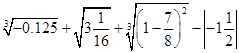
(3)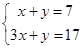 (4)
(4)
如图,直线y= x+m与抛物线y=
x+m与抛物线y= x2-2x+l交于不同的两点M、N(点M在点N的左侧).
x2-2x+l交于不同的两点M、N(点M在点N的左侧).
(1)设抛物线的顶点为B,对称轴l与直线y= x+m的交点为C,连结BM、BN,若S△MBC=
x+m的交点为C,连结BM、BN,若S△MBC= S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;
(2)在(1)条件下,已知点P(t,0)为x轴上的一个动点,
①若△PMN为直角三角形,求点P的坐标.
②若∠MPN>90°,则t的取值范围是.