（·辽宁营口）某化妆品专卖店，为了吸引顾客，在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动，凡购物满88元，均可得到一次摇奖的机会．已知在摇奖机内装有2个红球和2个白球，除颜色外其它都相同，摇奖者必须从摇奖机中一次连续摇出两个球，根据球的颜色决定送礼金券的多少（如下表）：
| 甲种品牌 化妆品 |
球 |
两红 |
一红一白 |
两白 |
| 礼金卷（元） |
6 |
12 |
6 |
| 乙种品牌 化妆品 |
球 |
两红 |
一红一白 |
两白 |
| 礼金卷（元） |
12 |
6 |
12 |
（1）请你用列表法（或画树状图法）求一次连续摇出一红一白两球的概率；
（2）如果一个顾客当天在本店购物满88元，若只考虑获得最多的礼品卷，请你帮助分析选择购买哪种品牌的化妆品？并说明理由．
一段圆弧形公路弯道，圆弧的半径为2km，弯道所对圆心角为10°，一辆汽车从此弯道上驶过，用时20 s，弯道有一块限速警示牌，限速为40km/h，问这辆汽车经过弯道时有没有超速？（π取3）
如图，在平面直角坐标系中，抛物线经过A(-1，0),B(4，0),C(0，-4),⊙M是△ABC的外接圆，M为圆心。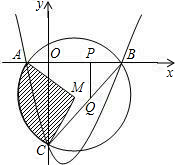
⑴求抛物线的解析式；
⑵求阴影部分的面积；
⑶在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=K,△CPQ的面积为S,求S关于K的函数关系式，并求出S的最大值。
如图，在平面直角坐标系中，已知点A(0，12),B(16，0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动，同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动，设点P、Q移动的时间为t秒。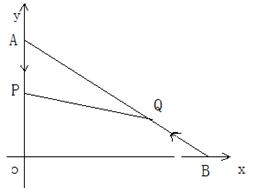
⑴求直线AB的解析式；
⑵求t为何值时，△APQ与△AOB相似？
⑶当t为何值时，△APQ的面积为
个平方单位？
⑷当t为何值时，△APQ的面积最大，最大值是多少？
动物园计划用长为120米的铁丝围成如图所示的兔笼，（不包括顶棚）供学习小组的同学参观，其中一面靠墙，（墙足够长）怎样设计围成的面积最大？
如图，点A,B,C,D在⊙O上，AB=AC,AD与BC相交于点E,AE=
ED,延长DB到点F,使DB到点F,使FB=BD,连接AF.
⑴△BDE∽△FDA;
⑵试判断直线AF与⊙O的位置关系，并给出证明。