(·辽宁丹东).如图,AB是⊙O的直径,弧ED=弧BD,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.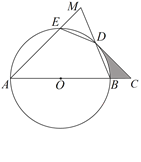
(1)若OA CD
CD
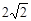 ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE DM.
DM.
如图, 为线段 外一点.
(1)求作四边形 ,使得 ,且 ;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的四边形 中, , 相交于点 , , 的中点分别为 , ,求证: , , 三点在同一条直线上.

为贯彻落实党中央关于全面建成小康社会的战略部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.经过多年的精心帮扶,截至2019年底,按照农民人均年纯收入3218元的脱贫标准,该地区只剩少量家庭尚未脱贫.现从这些尚未脱贫的家庭中随机抽取50户,统计其2019年的家庭人均年纯收入,得到如图1所示的条形图.

(1)如果该地区尚未脱贫的家庭共有1000户,试估计其中家庭人均年纯收入低于2000元(不含2000元)的户数;
(2)估计2019年该地区尚未脱贫的家庭人均年纯收入的平均值;
(3)2020年初,由于新冠疫情,农民收入受到严重影响,上半年当地农民家庭人均月纯收入的最低值变化情况如图2的折线图所示.为确保当地农民在2020年全面脱贫,当地政府积极筹集资金,引进某科研机构的扶贫专项项目.据预测,随着该项目的实施,当地农民自2020年6月开始,以后每月家庭人均月纯收入都将比上一个月增加170元.

已知2020年农村脱贫标准为农民人均年纯收入4000元,试根据以上信息预测该地区所有贫困家庭能否在今年实现全面脱贫.
如图, 与 相切于点 , 交 于点 , 的延长线交 于点 , 是 上不与 , 重合的点, .
(1)求 的大小;
(2)若 的半径为3,点 在 的延长线上,且 ,求证: 与 相切.

某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和都是100吨,且甲特产的销售量都不超过20吨.
(1)若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?
(2)求该公司一个月销售这两种特产所能获得的最大总利润.
先化简,再求值: ,其中 .