(·辽宁大连)如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE.设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C、F、D的抛物线为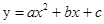 .
.
(1)求点D的坐标(用含m的式子表示)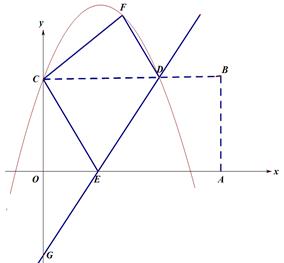
(2)若点G的坐标为(0,-3),求该抛物线的解析式.
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=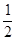 EA?若存在,直接写出P的坐标,若不存在,说明理由.
EA?若存在,直接写出P的坐标,若不存在,说明理由.
如图①所示,直线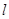 :
: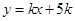 与
与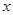 轴负半轴、
轴负半轴、 轴正半轴分别交于
轴正半轴分别交于 、
、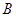 两点.(1)当
两点.(1)当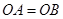 时,试确定直线
时,试确定直线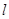 的解析式;
的解析式;
(2)在(1)的条件下,如图②所示,设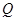 为
为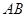 延长线上一点,连接
延长线上一点,连接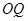 ,过
,过 、
、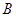 两点分别作
两点分别作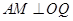 于
于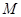 ,
,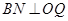 于
于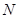 ,若
,若 ,求M点的坐标;
,求M点的坐标;
(3)当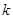 取不同的值时,点
取不同的值时,点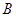 在
在 轴正半轴上运动,分别以
轴正半轴上运动,分别以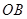 、
、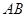 为边在第一、第二象限作等腰直角
为边在第一、第二象限作等腰直角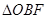 和等腰直角
和等腰直角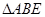 ,连
,连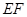 交
交 轴于
轴于 点,问当点
点,问当点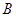 在
在 轴上运动时,试猜想△ABP的面积是否改变,若不变,请求出其值;若改变,请说明理由.
轴上运动时,试猜想△ABP的面积是否改变,若不变,请求出其值;若改变,请说明理由.
(4)当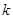 取不同的值时,点
取不同的值时,点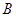 在
在 轴正半轴上运动,以
轴正半轴上运动,以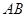 为边在第二象限作等腰直角
为边在第二象限作等腰直角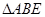 ,则动点E在直线_______________________________上运动.(直接写出直线的表达式)
,则动点E在直线_______________________________上运动.(直接写出直线的表达式)
甲、乙两车同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程y(千米)与行驶时间x(时)的函数图象如图所示.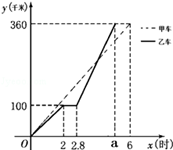
(1)乙车到达B地所用的时间a的值为 ;
(2)行驶过程中,两车出发多长时间后首次相遇?
(3)当x=3时,甲、乙两车之间的距离是 千米;
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.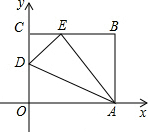
(1)求CE和OD的长;
(2)求直线DE的表达式;
(3)直线y=kx+b与DE平行,当它与矩形OABC有公共点时,直接写出b的取值范围.
某蒜薹(tái)生产基地喜获丰收,收获蒜薹200吨,经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并且按这三种方式销售,计划每吨平均的售价及成本如下表:
| 销售方式 |
批发 |
零售 |
储藏后销售 |
| 售价(百元/吨) |
3 0 |
4 5 |
5 5 |
| 成本(百元/吨) |
7 |
1 0 |
1 2 |
若蒜薹按计划全部售出获得的总利润为y(百元),蒜薹零售x(吨),且批发量是零售量的3倍.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
计算
(1)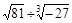 -
-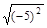 ;
;
(2)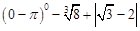
(3)解方程: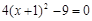 .
.