(·辽宁本溪)如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
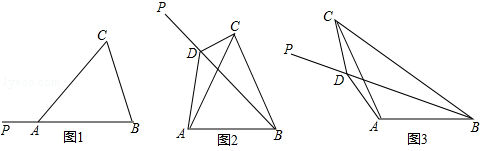
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=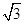 AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
桌面上有5张背面相同的卡片,正面分别写着数字“1”、“2”、“3”、“4”、 “5”.将卡片背面朝上洗匀.
(1)小军从中任意抽取一张,抽到偶数的概率是;
(2)小红从中同时抽取两张.规定:抽到的两张卡片上的数字之和为奇数,则小军胜,否则小红胜.你认为这个游戏公平吗?请用树状图或表格说明你的理由.
南京市为了构建立体的道路网络,大力发展江北经济,决定修建一条六合到主城的轻轨铁路.为了使工程提前3个月完成,需将原定的工作效率提高10%.原计划完成这项工程需要多少个月?
下列为某校初三参加的“迎青奥”知识能力竞赛的25位同学的成绩:
78,86,98,90,95, 88,94,80,89,77, 87,73,65,84,87,
96,84,74,98,86, 83,67,88,68,85.
(1)完成下表:
(2)补全频数分布直方图;
(3)若超过均分的将获奖,请计算本次竞赛获奖的比例.
如图,四边形ABCD为矩形,四边形AEDF为菱形.
(1)求证:△ABE≌△DCE;
(2)试探究:当矩形ABCD边长满足什么关系时,菱形AEDF为正方形?请说明理由.
先化简,再求值:[(a-2)2-(a+2)(a-2)](a-1),其中a=-2.