(·黑龙江大庆)小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据: ,
, .结果保留整数)
.结果保留整数)
(本小题满分8分)在全市中学运动会800m比赛中,甲乙两名运动员同时起跑,刚跑出200m后,甲不慎摔倒,他又迅速地爬起来继续投入比赛,并取得了优异的成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系,根据图像解答下列问题:
(1)甲摔倒前,________的速度快(填甲或乙);
(2)甲再次投入比赛后,在距离终点多远处追上乙?
(本小题满分8分)如图,一次函数 的图象与反比例函数
的图象与反比例函数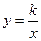 的图象交于
的图象交于 两点,与
两点,与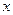 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知 ,
,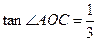 ,点
,点 的坐标为
的坐标为 .
.
(1)求反比例函数的解析式.
(2)求一次函数的解析式.
(3)在 轴上存在一点
轴上存在一点 ,使得
,使得 与
与 相似,请你求出
相似,请你求出 点的坐标.
点的坐标.
(本小题满分8分)小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片 放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知
放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知 =36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
(本题共两小题,每小题6分,满分12分)
(1)计算: .
.
(2)解不等式组,并把解集在数轴上表示出来.

(本小题满分12分)如图1,已知抛物线经过坐标原点 和
和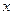 轴上另一点
轴上另一点 ,顶点
,顶点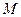 的坐标为
的坐标为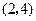 ;矩形
;矩形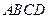 的顶点
的顶点 与点
与点 重合,
重合, 分别在
分别在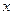 轴、
轴、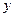 轴上,且
轴上,且 ,
, .
.
(1)求该抛物线所对应的函数关系式;
(2)将矩形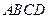 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿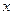 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点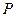 也以相同的速度从点
也以相同的速度从点 出发向
出发向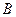 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为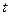 秒(
秒( ),直线
),直线 与该抛物线的交点为
与该抛物线的交点为 (如图2所示).
(如图2所示).
①当 时,判断点
时,判断点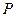 是否在直线
是否在直线 上,并说明理由;
上,并说明理由;
②设以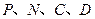 为顶点的多边形面积为
为顶点的多边形面积为 ,试问
,试问 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.