（·黑龙江牡丹江）已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．
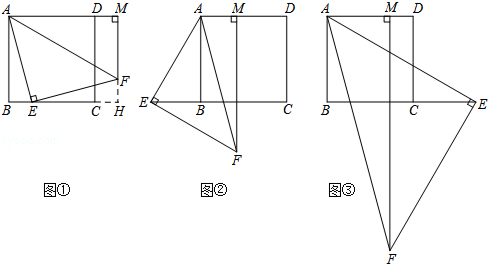
（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；
（提示：延长MF，交边BC的延长线于点H．）
（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；
（3）在（1），（2）的条件下，若BE=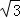
，∠AFM=15°，则AM= ．
为支持亚太地区国家基础设施建设，由中国倡议设立亚投行，截止2015年4月15日，亚投行意向创始成员国确定为57个，其中意向创始成员国数亚洲是欧洲的2倍少2个，其余洲共5个，求亚洲和欧洲的意向创始成员国各有多少个？
现正是闽北特产杨梅热销的季节，某水果零售商店分两批次从批发市场共购进杨梅40箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款700元．
（1）设第一、二次购进杨梅的箱数分别为a箱、b箱，求a，b的值；
（2）若商店对这40箱杨梅先按每箱60元销售了x箱，其余的按每箱35元全部售完．
①求商店销售完全部杨梅所获利润y（元）与x（箱）之间的函数关系式；
②当x的值至少为多少时，商店才不会亏本．
（注：按整箱出售，利润=销售总收入﹣进货总成本）
解分式方程：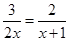
．
有48支队520名运动员参加篮球、排球比赛，其中每支篮球队10人，每支排球队12人， 每名运动员只能参加一项比赛，篮球、排球队各有多少支参赛?
已知关于x的方程x2+（2m-1）+4=0有两个相等的实数根，求m的值．