如图,抛物线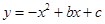 交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且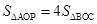 ,求点P的坐标;
,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
如图,已知BC∥GE,AF∥DE,∠1=50°.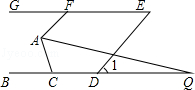
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)九年级(1)班体育测试的人数为 ;
(2)请把条形统计图补充完整;
(3)扇形统计图中A级所在的扇形的圆心角度数是 ;
(4)若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数约为多少人?
(1)解方程组:
(2)解方程:
(3)已知10m=2,10n=3,求102m+n的值.
(1)(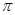 -3)0-(-
-3)0-(- )-2+(-1)2015
)-2+(-1)2015
(2)2a2b•(-3b2c)÷(4ab3)
“鸡兔同笼”是我国民间流传的诗歌形式的数学题:“鸡兔同笼不知数,三十六头笼中露,看来脚有100只,几多鸡儿几多兔”解决此问题,设鸡为x只,兔为y只,则所列方程组正确的是()
A. |
B. |
C. |
D. |