如图①，半径为R，圆心角为n°的扇形面积是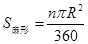
，由弧长l=
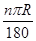，得=
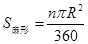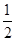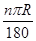••R=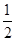lR．通过观察，我们发现S扇形=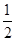lR类似于S三角形=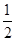×底×高．
类比扇形，我们探索扇环（如图②，两个同心圆围成的圆环被扇形截得的一部分交作扇环）的面积公式及其应用．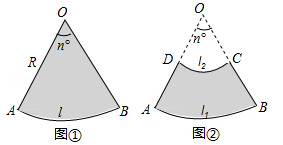
（1）设扇环的面积为S扇环，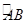
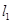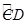的长为
，
的长为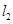
，线段AD的长为h（即两个同心圆半径R与r的差）．类比S梯形=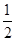×（上底+下底）×高，用含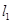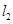，，h的代数式表示S扇环，并证明；
（2）用一段长为40m的篱笆围成一个如图②所示的扇环形花园，线段AD的长h为多少时，花园的面积最大，最大面积是多少？
计算下列各式：
（1）-1-2+4；
（2）
；
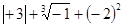（3）（-3）÷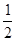
+
×（-
）；
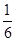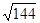（4）
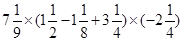
如图，已知抛物线y=x2+bx－3a过点A（1，0），B（0，－3），与x轴交于另一点C.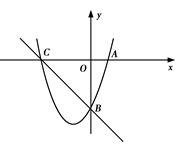
（1）求抛物线的解析式；
（2）若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，求点P的坐标；
（3）在（2）的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由.
已知：如图8，△ABC中，AC＝BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．（12）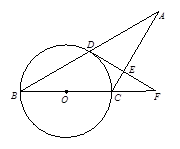
求证：（1）AD＝BD； （2）DF是⊙O的切线．
某商店经销一批小家电，每个小家电的成本为40元。据市场分析，销售单价定为50元时，一个月能售出500件；若销售单价每涨1元，月销售量就减少10件．针对这种小家电的销售情况，请回答以下问题：
（1）设销售单价定为x元（x>50），月销售利润为y元，求y(用含x的代数式表示)；
（2）现该商店要保证每月盈利8750元，同时又要使顾客得到尽可能多的实惠，那么销售单价应定为多少元？
如图1，平面直角坐标系中，抛物线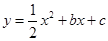
与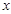
轴交于A、B两点，点C是AB的中点，CD⊥AB且CD=AB.直线BE与
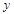轴平行，点F是射线BE上的一个动点，连接AD、AF、DF.
（1）若点F的坐标为（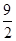
，
），AF=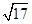
.
①求此抛物线的解析式；
②点P是此抛物线上一个动点，点Q在此抛物线的对称轴上，以点A、F、P、Q为顶点构成的四边形是平行四边形，请直接写出点Q的坐标；
（2）若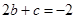
，
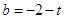，且AB的长为
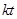，其中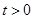
.如图2，当∠DAF=45时，求
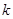的值和∠DFA的正切值.