如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.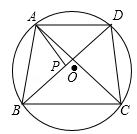
(1)AB=CD;
(2)DP•BD=AD•BC;
(3)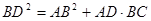 .
.
如图,有一张边长为 米的正方形硬纸张,现将四个角截去四个边长为
米的正方形硬纸张,现将四个角截去四个边长为 米的小正方形,然后折成一个无盖的长方体盒子.(
米的小正方形,然后折成一个无盖的长方体盒子.( >2
>2 >0)
>0)
(1)直接写出盒子底面边长的长度;(用含 、
、 的代数式表示)
的代数式表示)
(2)截去四个小正方形后,剩余硬纸张的面积S为多少平方米?请用含 、
、 的代数式表示出来,并把此代数式分解因式;
的代数式表示出来,并把此代数式分解因式;
(3)若无盖长方体盒子的体积为 立方米,且截去四个小正方形后,剩余硬纸张的面积为
立方米,且截去四个小正方形后,剩余硬纸张的面积为 平方米,求
平方米,求 、
、 的值.
的值.
一个正方形的边长增加 后的正方形面积比它的边长增加
后的正方形面积比它的边长增加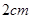 后的面积多
后的面积多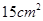 .若设原来这个正方形的边长为
.若设原来这个正方形的边长为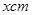 ,
,
(1)当边长增加3 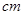 时,则正方形的面积为
时,则正方形的面积为 ;当边长增加
;当边长增加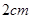 后,正方形的面积为
后,正方形的面积为 .(均用含
.(均用含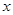 的代数式表示)
的代数式表示)
(2)求原来这个正方形的面积
已知 ,
,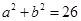 .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
先化简,再求值(每小题6分,计12分):
(1) ,其中
,其中 ;
;
(2)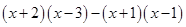 ,其中
,其中 =-2。
=-2。
(本小题10分)已知二次函数 ( b,c为常数).
( b,c为常数).
(Ⅰ)当b =2,c =-3时,求二次函数的最小值;
(Ⅱ)当c =5时,若在函数值y =1的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;
(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.