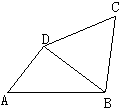
两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
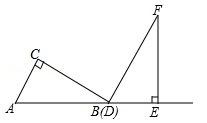
(1)当点C落在边EF上时,x= cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.
计算:sin30°+cos60°-tan45°-tan30°·tan60°
计算:tan60°·cos30°-3tan30°·tan45°
探究:
(1)a克糖水中有b克糖(a>b>0),则糖的质量与糖水质量的比为_______; 若再添加c克糖(c>0),则糖的质量与糖水的质量的比为________.生活常识告诉我们: 添加的糖完全溶解后,糖水会更甜,请根据所列式子及这个生活常识提炼出一个不等式: ____________.
(2)我们知道山坡的坡角越大,则坡越陡,联想到课本中的结论:tanA的值越大, 则坡越陡,我们会得到一个锐角逐渐变大时,它的正切值随着这个角的变化而变化的规律,请你写出这个规律:_____________.
(3)如图,在Rt△ABC中,∠B=90°,AB=a,BC=b(a>b),延长BA、BC,使AE="CD=c," 直线CA、DE交于点F,请运用(2) 中得到的规律并根据以上提供的几何模型证明你提炼出的不等式.
已知:如图,斜坡AB的倾斜角a,且tanα=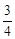 ,现有一小球从坡底A处以20cm/s 的速度向坡顶B处移动,则小球以多大的速度向上升高?
,现有一小球从坡底A处以20cm/s 的速度向坡顶B处移动,则小球以多大的速度向上升高?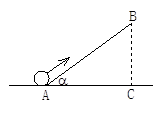
如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD= .求:
.求: 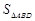 :
: 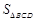 .
.