(本小题满分11分)
如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.

(本题10分).如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.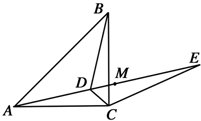
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
(本题10分)已知:如图所示,(1)作出△ABC关于y轴对称的△
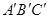 ,并写出△
,并写出△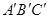 三个顶点的坐标.
三个顶点的坐标.(2) 在x轴上画出点P,使PA+PC最小.

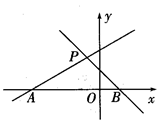
(本题10分)如图,直线x-2y=-5和x+y=1分别与x轴交于A、B两点,这两条线的交点为P.(1)求点P的坐标.
(2)求△APB的面积.
(6分)我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数。(1)试举一个例子来判断上述猜测结论是否成立;(2分)
(2)若
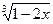 与
与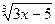 互为相反数,求1-
互为相反数,求1-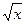 的值。(4分)
的值。(4分)
(本题8分)如图,在4×3的网格上,由个数相同的白色方块与黑色方块组成一幅图案,请仿照此图案,在下列网格中分别设计出2个轴对称图案(注:①不得与原图案相同;②黑、白方块的个数要相同).