（本小题满分10分）
问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
问题探究：不妨假设能搭成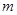种不同的等腰三角形，为探究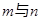之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．
探究一：
（1）用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当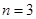时，
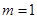
（2）用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当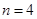时，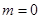
（3）用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当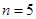时，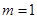
（4）用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当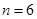时，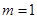
综上所述，可得表①

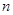	3	4	5	6
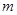	1	0	1	1

探究二：
（1）用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（仿照上述探究方法，写出解答过程，并把结果填在表②中）
（2）分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（只需把结果填在表②中）

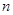	7	8	9	10

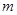你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用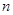根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
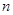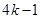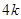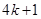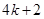（设分别等于、、、，其中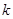是整数，把结果填在表③中）

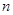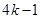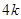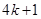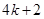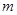问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
（要求写出解答过程）
其中面积最大的等腰三角形每个腰用了_______________根木棒。（只填结果）

科目 数学   题型 解答题   难度 中等