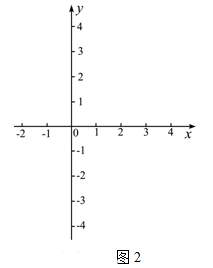（1）请补全以下求不等式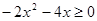
的解集的过程．
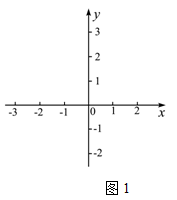
①构造函数，画出图象：根据不等式特征构造二次函数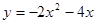
；并在下面的坐标系中（见图1）画出二次函数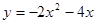的图象（只画出图象即可）．
②求得界点，标示所需：当y=0时，求得方程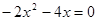
的解为 ；并用锯齿线标示出函数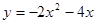图象中y≥0的部分．
③借助图象,写出解集：由所标示图象，可得不等式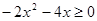的解集为 ．
（2）利用（1）中求不等式解集的步骤,求不等式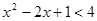
的解集．
①构造函数，画出图象：
②求得界点，标示所需：
③借助图像，写出解集：
（3）参照以上两个求不等式解集的过程,借助一元二次方程的求根公式，直接写出关于x的不等式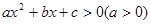
的解集．
，
分别满足
，
，且
的值。
0
