某射击运动员在一次比赛中,前6次射击已经得到52环,该项目的记录是89环(10次射击,每次射击环数只取1~10中的正整数).
(1)如果他要打破记录,第7次射击不能少于多少环?
(2)如果他第7次射击成绩为8环,那么最后3次射击中要有几次命中10环才能打破记录?
(3)如果他第7次射击成绩为10环,那么最后3次射击中是否必须至少有一次命中10环才有可能打破记录?
(每小题5分,共10分)
(1)化简:  +
+ —
— (2)求x的值:
(2)求x的值:
在平面直角坐标系xOy中,已知抛物线 的对称轴是
的对称轴是 ,并且经过(-2,-5)和(5,-12)两点.
,并且经过(-2,-5)和(5,-12)两点.
(1)求此抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,D是线段BC上一点(不与点B、C重合),若以B、O、D为顶点的三角形与△BAC相似,求点D的坐标;
(3)点P在y轴上,点M在此抛物线上,若要使以点P、M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标.
在平面直角坐标系xOy中,反比例函数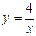 的图象与抛物线
的图象与抛物线
交于点A(3, n).
(1)求n的值及抛物线的解析式;
(2) 过点A作直线BC,交x轴于点B,交反比例函数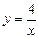 (
( )的图象于点C,且AC=2AB,求B、C两点的坐标;
)的图象于点C,且AC=2AB,求B、C两点的坐标;
(3)在(2)的条件下,若点P是抛物线对称轴上的一点,且点P到x轴和直线BC的距离相等,求点P的坐标.
如图,在△ABC中,∠C=60°,BC=4,AC=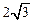 ,点P在BC边上运动,PD∥AB,交AC于D. 设BP的长为x,△APD的面积为y .
,点P在BC边上运动,PD∥AB,交AC于D. 设BP的长为x,△APD的面积为y .
(1)求AD的长(用含x的代数式表示);
(2)求y与x之间的函数关系式,并回答当x取何值时,y的值最大?最大值是多少?
(3)点P是否存在这样的位置,使得△ADP的面积是△ABP面积的 ?若存在,请求出BP的长;若不存在,请说明理由.
?若存在,请求出BP的长;若不存在,请说明理由.
(本小题满分4分)
如图,已知每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形. 图中的△ABC是一个格点三角形.
(1)请你在第一象限内画出格点△AB1C1, 使得△AB1C1∽△ABC,且△AB1C1与△ABC的相似比为3:1;
(2)写出B1、C1两点的坐标.