(本小题满分9分)为提高饮水质量,越来越多的居民开始选购家用净水器,一商场抓住商机,从厂家购进A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元,
(1)求A、B两种型号家用净水器各购进多少台?
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价-进价)
某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
(1)解方程: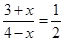 ;
;
(2)解不等式组: .
.
(1)计算: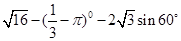 ;
;
(2)化简: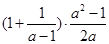 .
.
端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2,其中ab=﹣ .
.