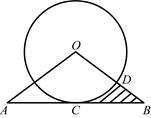
已知:在直角坐标平面内,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)
(1)在备用图(1)中,画出△ABC向下平移4个单位长度得到△A B
B C
C ,点C
,点C 的坐标是________.
的坐标是________.
(2)在备用图(2)中,以点B为位似中心,在网格内画出△A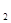 B
B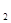 C
C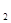 ,使△A
,使△A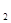 B
B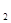 C
C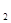 与△ABC位似,且位似比为2︰1,点C
与△ABC位似,且位似比为2︰1,点C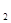 的坐标是________.
的坐标是________.
(3)△A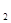 B
B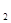 C
C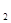 的面积是________平方单位.
的面积是________平方单位.

已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:如调整价格 ,每涨价一元,每星期要少卖出10件。该商品应定价为多少元时,商场能获得最大利润?
函数y =ax²(a≠0)与直线y =2x-3的图像交于点(1,b).
求:(1)a和b的值;
(2)求抛物线y =ax²的开口方向、对称轴、顶点坐标。
已知二次函数的图象经过点(0,- 3),且顶点坐标为(1,- 4).求这个解析式。
一布袋中有红、黄、白三种颜色的球各一个,它们除颜色外,其它都一样,小亮从布袋摸出一个球后放回去摇匀,再摸出一个球,请你用列举法(列表法或树形图)分析并求出小亮两次都能摸到白球的概率。
如图,线段 与⊙O相切于点
与⊙O相切于点 ,连结
,连结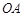 、
、 ,
, 交⊙O于点D,已知OA=OB=6cm,AB=
交⊙O于点D,已知OA=OB=6cm,AB= cm.
cm.
求:(1)⊙O的半径;
(2)图中阴影部分的面积.