如图，在△ABC中，∠ABC=90°，以AB的中点为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．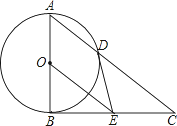
（1）判断DE与⊙O的位置关系，并说明理由；
（2）求证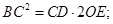
（3）若cos∠BAD=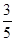
，BE=6，求OD的长．
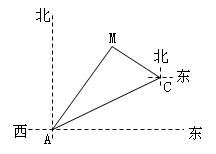
如图，某天然气公司的主输气管道从A市的北偏东60°方向直线延伸，测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向，测绘员沿主输气管道步行2000米到达C处，测得小区M位于C的北偏西60°方向，请你在主输气管道上寻找支管道连接点N，使到该小区铺设的管道最短，并求AN的长．(结果保留根号)
|
|
已知一个三角形的两边分别为
，这两边的夹角为
，请用尺规作图法作出这个三角形．(要求：写出已知、求作，保留作图痕迹，不写作法，最后要作答)
解方程组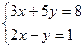
如图，以Rt△ABO的直角顶点O为原点，OA所在的直线为x轴，OB所在的直线为y轴，建立平面直角坐标系．已知OA=4，OB=3，一动点P从O出发沿OA方向，以每秒1个
单位长度的速度向A点匀速运动，到达A点后立即以原速沿AO返回；点Q从A点出发
沿AB以每秒1个单位长度的速度向点B匀速运动．当Q到达B时，P、Q两点同时停止
运动,设P、Q运动的时间为t秒(t＞0)．
(1) 试求出△APQ的面积S与运动时间t之间的函数关系式；
(2) 在某一时刻将△APQ沿着PQ翻折，使得点A恰好落在AB边的点D处，如图①．
求出此时△APQ的面积．
(3) 在点P从O向A运动的过程中，在y轴上是否存在着点E使得四边形PQBE为等腰梯
形？若存在，求出点E的坐标；若不存在，请说明理由．
(4) 伴随着P、Q两点的运动，线段PQ的垂直平分线DF交PQ于点D，交折线QB－BO－OP于点F． 当DF经过原点O时，请直接写出t的值．