如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.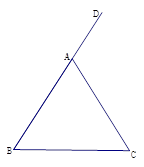
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)你认为图②中的阴影部分的正方形的边长等于_________________
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出 这三个代数式之间的等量关系吗?
这三个代数式之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求 .
.
如图,将连续的奇数1、3、5、7 …… ,排列成如下的数表,用十字框框出5个数。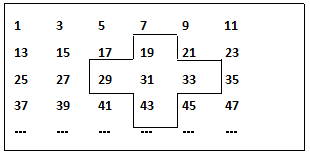
问:(1)十字框框出5个数字的和与框子正中间的数31有什么关系?
(2)若将十字框上下左右平移,可框住另外5个数,若设中间的数为a,用代数式表示十字框框住的5个数字之和;
(3)十字框框住的5个数字之和能等于2000吗?若能,分别写出十字框框住的5个数;若不能,请说明理由。
七年级学生在5名教师的带领下去公园秋游.公园的门票为每人30元,现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用代数式表示两种优惠方案各需多少费用?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
有 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
回答下列问题:
(1)这 筐白菜中最接近标准重量的这筐白菜重千克;
筐白菜中最接近标准重量的这筐白菜重千克;
(2)这 筐白菜一共重多少千克?
筐白菜一共重多少千克?
先化简,再求值: