已知:在直角坐标平面内,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)
(1)在备用图(1)中,画出△ABC向下平移4个单位长度得到△A B
B C
C ,点C
,点C 的坐标是________.
的坐标是________.
(2)在备用图(2)中,以点B为位似中心,在网格内画出△A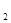 B
B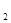 C
C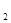 ,使△A
,使△A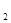 B
B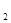 C
C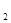 与△ABC位似,且位似比为2︰1,点C
与△ABC位似,且位似比为2︰1,点C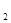 的坐标是________.
的坐标是________.
(3)△A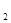 B
B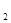 C
C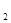 的面积是________平方单位.
的面积是________平方单位.

先化简(6x +
+ 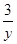
 -(4y
-(4y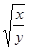 +
+ 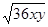 )再求值,其中
)再求值,其中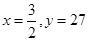
先阅读,后解答:
像上述解题过程中, 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1) 的有理化因式是;
的有理化因式是; 的有理化因式是。
的有理化因式是。
(2)将下列式子进行分母有理化:
① =;②
=;② =。
=。
(3)已知 ,比较
,比较 与
与 的大小关系。
的大小关系。
若x=0是关于x的一元二次方程 的解,求实数m的值,并解此方程.
的解,求实数m的值,并解此方程.
画图: 已知:点C是∠AOB的边OB上的一点,过点C作OA的垂线PC,与OA交与点P,在PC上求作一点Q,使该点到∠AOB的两边的距离相等。
一布袋中有红、黄、白三种颜色的球各一个,它们除颜色外其它都一样。小亮从布袋中摸出一个球后放回去摇匀,再摸出一个球。请你利用列举法(列表或画树状图)分析并求出小亮两次都能摸到白球的概率。