【问题提出】
如图①，已知⊿ABC是等边三角形，点E在线段AB上，点D在直线BC上，且DE=EC，将⊿BCE绕点C顺时针旋转
至⊿ACF，连接EF。
试证明：AB=DB+AF。
【类比探究】
（1）如图②，如果点E在线段AB的延长线上，其它条件不变，线段AB、DB、AF之间又有怎样的数量关系？请说明理由。
（2）如果点E在线段BA的延长线上，其他条件不变，请在图③的基础上将图形补充完整，并写出AB，DB，AF之间数量关系，不必说明理由。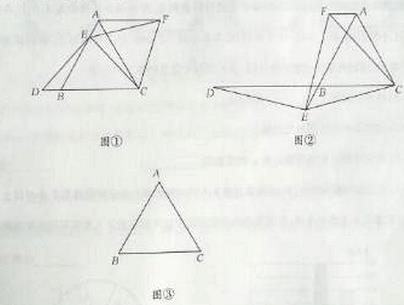
先化简，再求值：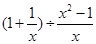
，其中x=2．
尺规作图：画出线段AB的垂直平分线（不写作法，保留作图痕迹）
解方程组
．
在平面直角坐标系中，点O为原点，抛物线y=ax2+bx（其中-1≤a＜0）经过A（3，n），AB⊥y轴于B，抛物线交直线AB于M．
（1）若n=1，AB=3BM，求抛物线所对应的函数关系式；
（2）若n=a+b，抛物线与x轴另一个异于原点的交点为C，过点A作AP∥OM交直线MC于点P，当△OPM的面积最大时，求sin∠MOP的值．
如图，四边形ABCD是⊙O的内接四边形，
，点E、F分别是弦AD、DC上的点．
（1）若∠ABE=∠CBF，BE=BF．求证：BD是⊙O的直径．
（2）若
，∠D=2∠EBF=90°，AE=ED=2．求DF的长．