(自贡)解不等式: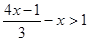 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
如图,将等腰直角三角形纸片 对折,折痕为 .展平后,再将点 折叠在边 上(不与 、 重合),折痕为 ,点 在 上的对应点为 ,设 与 交于点 ,连接 .已知 .
(1)若 为 的中点,求 的长;
(2)随着点 在边 上取不同的位置,
① 的形状是否发生变化?请说明理由;
②求 的周长的取值范围.

如图,在平面直角坐标系中,二次函数 的图象与 轴交于 、 两点,与 轴交于点 ,其顶点为 ,连接 、 、 ,过点 作 轴的垂线 .
(1)求点 , 的坐标;
(2)直线 上是否存在点 ,使 的面积等于 的面积的2倍?若存在,求出点 的坐标;若不存在,请说明理由.

如图,1号楼在2号楼的南侧,两楼高度均为 ,楼间距为 .冬至日正午,太阳光线与水平面所成的角为 ,1号楼在2号楼墙面上的影高为 ;春分日正午,太阳光线与水平面所成的角为 ,1号楼在2号楼墙面上的影高为 .已知 .
(1)求楼间距 ;
(2)若2号楼共30层,层高均为 ,则点 位于第几层?(参考数据: , , , , ,

如图, 为 的直径,点 在 外, 的平分线与 交于点 , .
(1) 与 有怎样的位置关系?请说明理由;
(2)若 , ,求 的长.

徐州至北京的高铁里程约为 ,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁 与“复兴号”高铁 前往北京.已知 车的平均速度比 车的平均速度慢 , 车的行驶时间比 车的行驶时间多 ,两车的行驶时间分别为多少?