(南充)已知抛物线 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线 (
( )与抛物线相交于两点M(
)与抛物线相交于两点M( ,
, ),N(
),N( ,
, )(
)(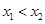 ),当
),当 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.
如图,在矩形
中,点
在边
上,且
,过点
作
,垂足为点
.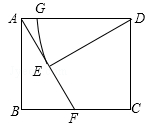
(1)求证:
;
(2)以
为圆心,
为半径作圆弧交
于点
.若
,试求
的长.
小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题: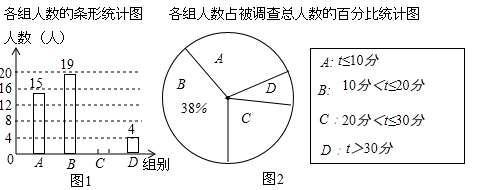
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.
在平面直角坐标系中,点
的坐标是(0,3),点
在
轴上,将
绕点
逆时针旋转90°得到
,点
、
的对应点分别是点
、
.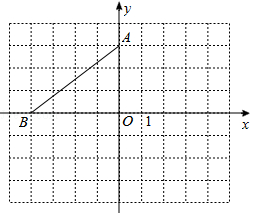
(1)若点
的坐标是
,请在图中画出
,并写出点
、
的坐标.
(2)当点
落在
轴的上方时,试写出一个符合条件的点
的坐标.
解不等式组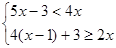 .
.
图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC′D′,最后折叠形成一条线段BD″.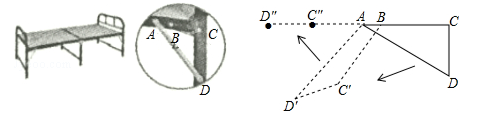
(1)小床这样设计应用的数学原理是.
(2)若AB:BC=1:4,则tan∠CAD的值是.