如图甲所示，在竖直平面内有一个直角三角形斜面体，倾角θ为300，斜边长为x0，以斜面顶部O点为坐标轴原点，沿斜面向下建立一个一维坐标x轴。斜面顶部安装一个小的滑轮，通过定滑轮连接两个物体A、B（均可视为质点），其质量分别为m1、m2，所有摩擦均不计，开始时A处于斜面顶部，并取斜面底面所处的水平面为零重力势能面，B物体距离零势能面的距离为
；现在A物体上施加一个平行斜面斜向下的恒力F，使A由静止向下运动。当A向下运动位移x0时，B物体的机械能
随
轴坐标的变化规律如图乙，则结合图象可求：
（1）B物体最初的机械能E1和上升x0时的机械能E2；
（2）恒力F的大小。
如图所示。匀强电场的电场强度沿水平方向，现有质量为m、带电量为+q的一只带电小球，以速度V0沿向右偏上300的方向进入该电场，该小球恰好做直线运动。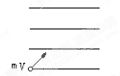
试求：（1）该电场的场强大小及方向。
（2）小球进入电场后在入射方向上的最大位移是多少？
如图所示。一端连着质量为m的小球的、长为L的轻杆另一端连在水平光滑轴O上，可在竖直面内转动。当小球运动至最高点A时，杆对小球的拉力大小为mg/2，则当小球运动至最低点B时，杆对小球的拉力大小为多少？
如图所示。在光滑绝缘的水平面上，三个带电小球a、b和c分别位于边长为L的正三角形的三个顶点上：a、b带正电，电量均为q，c带负电。整个系统置于方向水平的匀强电场中。已知静电力常量为K。若三个小球均处于静止状态，试求该匀强电场的场强以及C的带电量。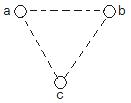
双星系统由两颗彼此相距很近的两个恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的共同质量中心做周期相同的匀速圆周运动。现有一个天文观测活动小组为了测量一双星系统中的两个恒星的质量m1和m2，进行了如下测量：测出了该双星系统的周期T和质量为m1和m2的两个恒星的运动半径r1和r2。是根据上述测量数据计算出两个恒星的质量m1和m2。（万有引力恒量为G）
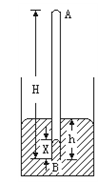
如图所示。把上端A封闭、下端B开口的长为H＝100cm的粗细均匀的玻璃管竖直缓慢地插入一个大水银槽中，插入的深度为h＝25cm。则进入玻璃管中的水银柱的长为多少？（大气压为75cmHg）