(广安)为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表: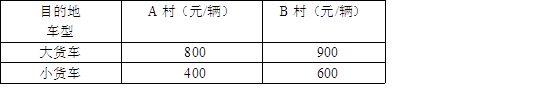
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
如图,正方形OABC的面积为9,点O为坐标原点,点B在函数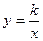
(k>0,x>0)的图象上,点P(m、n)是函数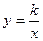 (k>0,x>0)的图象上任意一点,
(k>0,x>0)的图象上任意一点,
过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.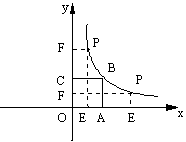
(1)求B点坐标和k的值;
(2)当S=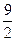 时,求点P的坐标。
时,求点P的坐标。
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D。
试说明:AC∥DF。
解:因为 ∠1=∠2(已知)
∠1=∠3,∠2=∠4()
所以∠3=∠4(等量代换)
所以 ∥()
所以 ∠C=∠ABD,()
又因为 ∠C=∠D(已知)
所以∠D=∠ABD(等量代换)
所以 AC∥DF()
如图,已知直线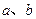 被直线
被直线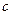 所截,
所截,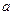 ∥
∥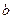 ,如果
,如果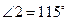 ,求∠1的度数。
,求∠1的度数。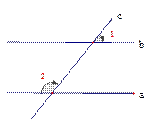
已知:如图,在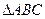 中,
中,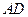 是
是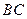 边上的高,
边上的高, 是
是 平分线.
平分线.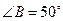 ,
,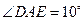 。
。
(1)求 的度数;
的度数;
(2)求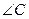 的度数.
的度数.
如图,△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,∠A=60°,
∠BDC=100°求∠BDE的度数。