如图，已知抛物线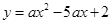
（
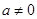）与y轴交于点C，与x轴交于点A（1，0）和点B．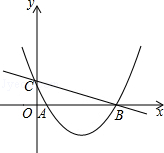
（1）求抛物线的解析式；
（2）求直线BC的解析式；
（3）若点N是抛物线上的动点，过点N作NH⊥x轴，垂足为H，以B，N，H为顶点的三角形是否能够与△OBC相似？若能，请求出所有符合条件的点N的坐标；若不能，请说明理由．
某中学八年级共有400名学生，学校为了增强学生的安全意识，在本年级进行了一次安全知识测验，为了了解这测验的成绩状况，从中抽取了50名学生的成绩，将所得数据整理后，画出频数分布直方图如图所示．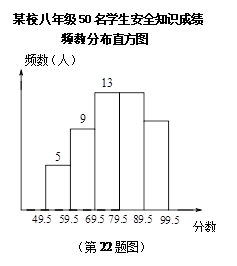
（1）图中成绩为79.5~89.5小组的频率是，成绩为89.5~99.5小组的频数是；
（2）这次测验中，假定成绩在70分以下为不合格，需重新学习安全知识，则八年级全体学生中需要重新学习的学生约为多少人？
如图，一道斜坡的坡比（BC与AC的长度之比）为1︰10，AC＝12m，求斜边AB的长（结果保留根号）．
在某一电路中，保持电压不变，电流I(安培)与电阻R(欧姆)成反比例，当电阻R=5欧姆时，电流I=2安培。
（1）求I与R之间的函数关系式
（2）当电流I=0.5安培时，求电阻R的值；
某少年军校的师生到距学校15千米的部队营地参观学习，一部分人骑自行车先走，过了40分钟后，其余的人乘汽车出发，结果他们同时到达，已知汽车的速度是自行车的速度的3倍，求这两种车的速度各是多少？
如图，一次函数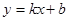
的图像与反比例函数
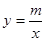的图像相交于A、B两点，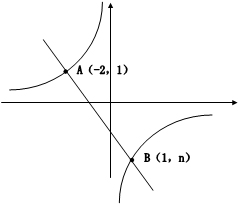
（1）利用图中条件，求反比例函数和一次函数的解析式
（2）根据图像写出使一次函数的值大于反比例函数的值的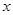
的取值范围